Как написать нейронную сеть на python?

Нейросеть на Python, часть 1

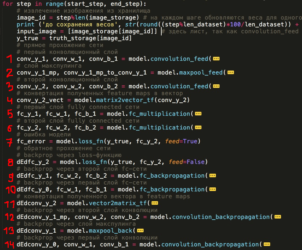
Лично я лучше всего обучаюсь при помощи небольшого работающего кода, с которым могу поиграться. В этом пособии мы научимся алгоритму обратного распространения ошибок на примере небольшой нейронной сети, реализованной на Python.

Нейросеть на Python

Дайте код!

X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ]) y = np.array([[0,1,1,0]]).T syn0 = 2*np.random.random((3,4)) — 1 syn1 = 2*np.random.random((4,1)) — 1 for j in xrange(60000): l1 = 1/(1+np.exp(-(np.dot(X,syn0)))) l2 = 1/(1+np.exp(-(np.dot(l1,syn1)))) l2_delta = (y — l2)*(l2*(1-l2)) l1_delta = l2_delta.dot(syn1.T) * (l1 * (1-l1)) syn1 += l1.T.dot(l2_delta) syn0 += X.T.dot(l1_delta)

Слишком сжато? Давайте разобьём его на более простые части.

Часть 1: Небольшая игрушечная нейросеть

Нейросеть, тренируемая через обратное распространение (backpropagation), пытается использовать входные данные для предсказания выходных.

Вход Выход 0 0 1 0 1 1 1 1 1 0 1 1 0 1 1 0

Предположим, нам нужно предсказать, как будет выглядеть колонка «выход» на основе входных данных. Эту задачу можно было бы решить, подсчитав статистическое соответствие между ними. И мы бы увидели, что с выходными данными на 100% коррелирует левый столбец.

Обратное распространение, в самом простом случае, рассчитывает подобную статистику для создания модели. Давайте попробуем.

Нейросеть в два слоя

import numpy as np def nonlin(x,deriv=False): if(deriv==True): return x*(1-x) return 1/(1+np.exp(-x)) X = np.array([ [0,0,1], [0,1,1], [1,0,1], [1,1,1] ]) y = np.array([[0,0,1,1]]).T np.random.seed(1) syn0 = 2*np.random.

random((3,1)) — 1 for iter in xrange(10000): l0 = X l1 = nonlin(np.dot(l0,syn0)) l1_error = y — l1 l1_delta = l1_error * nonlin(l1,True) syn0 += np.dot(l0.T,l1_delta) print «Выходные данные после тренировки:» print l1 Выходные данные после тренировки: [[ 0.00966449] [ 0.

00786506] [ 0.99358898] [ 0.99211957]]

Переменные и их описания.

X — матрица входного набор данных; строки – тренировочные примерыy – матрица выходного набора данных; строки – тренировочные примерыl0 – первый слой сети, определённый входными даннымиl1 – второй слой сети, или скрытый слойsyn0 – первый слой весов, Synapse 0, объединяет l0 с l1.“*” — поэлементное умножение – два вектора одного размера умножают соответствующие значения, и на выходе получается вектор такого же размера“-” – поэлементное вычитание векторов

И это работает! Рекомендую перед прочтением объяснения поиграться немного с кодом и понять, как он работает. Он должен запускаться прямо как есть, в ipython notebook. С чем можно повозиться в коде:

• сравните l1 после первой итерации и после последней
• посмотрите на функцию nonlin.
• посмотрите, как меняется l1_error
• разберите строку 36 – основные секретные ингредиенты собраны тут (отмечена !!!)
• разберите строку 39 – вся сеть готовится именно к этой операции (отмечена !!!)

Разберём код по строчкам

import numpy as np

Импортирует numpy, библиотеку линейной алгебры. Единственная наша зависимость.

def nonlin(x,deriv=False):

Наша нелинейность. Конкретно эта функция создаёт «сигмоиду». Она ставит в соответствие любое число значению от 0 до 1 и преобразовывает числа в вероятности, а также имеет несколько других полезных для тренировки нейросетей свойств.

if(deriv==True):

Эта функция также умеет выдавать производную сигмоиды (deriv=True). Это одно из её полезных свойств. Если выход функции – это переменная out, тогда производная будет out * (1-out). Эффективно.

X = np.array([ [0,0,1], …

Инициализация массива входных данных в виде numpy-матрицы. Каждая строка – тренировочный пример. Столбцы – это входные узлы. У нас получается 3 входных узла в сети и 4 тренировочных примера.

y = np.array([[0,0,1,1]]).T

Инициализирует выходные данные. “.T” – функция переноса. После переноса у матрицы y есть 4 строки с одним столбцом. Как и в случае входных данных, каждая строка – это тренировочный пример, и каждый столбец (в нашем случае один) – выходной узел. У сети, получается, 3 входа и 1 выход.

np.random.seed(1)

Благодаря этому случайное распределение будет каждый раз одним и тем же. Это позволит нам проще отслеживать работу сети после внесения изменений в код.

syn0 = 2*np.random.random((3,1)) – 1

Матрица весов сети. syn0 означает «synapse zero». Так как у нас всего два слоя, вход и выход, нам нужна одна матрица весов, которая их свяжет. Её размерность (3, 1), поскольку у нас есть 3 входа и 1 выход. Иными словами, l0 имеет размер 3, а l1 – 1. Поскольку мы связываем все узлы в l0 со всеми узлами l1, нам требуется матрица размерности (3, 1).

Заметьте, что она инициализируется случайным образом, и среднее значение равно нулю. За этим стоит достаточно сложная теория. Пока просто примем это как рекомендацию. Также заметим, что наша нейросеть – это и есть эта самая матрица. У нас есть «слои» l0 и l1, но они представляют собой временные значения, основанные на наборе данных. Мы их не храним. Всё обучение хранится в syn0.

for iter in xrange(10000):

l0 = X

Первый слой, l0, это просто данные. В X содержится 4 тренировочных примера. Мы обработаем их все и сразу – это называется групповой тренировкой [full batch]. Итого мы имеем 4 разных строки l0, но их можно представить себе как один тренировочный пример – на этом этапе это не имеет значения (можно было загрузить их 1000 или 10000 без всяких изменений в коде).

l1 = nonlin(np.dot(l0,syn0))

Это шаг предсказания. Мы позволяем сети попробовать предсказать вывод на основе ввода. Затем мы посмотрим, как это у неё получается, чтобы можно было подправить её в сторону улучшения.

В строке содержится два шага. Первый делает матричное перемножение l0 и syn0. Второй передаёт вывод через сигмоиду. Размерности у них следующие:

(4 x 3) dot (3 x 1) = (4 x 1)

Матричные умножения требуют, чтобы в середине уравнения размерности совпадали. Итоговая матрица имеет количество строк, как у первой, а столбцов – как у второй.

Мы загрузили 4 тренировочных примера, и получили 4 догадки (матрица 4х1). Каждый вывод соответствует догадке сети для данного ввода.

l1_error = y — l1

Поскольку в l1 содержатся догадки, мы можем сравнить их разницу с реальностью, вычитая её l1 из правильного ответа y. l1_error – вектор из положительных и отрицательных чисел, характеризующий «промах» сети.

l1_delta = l1_error * nonlin(l1,True)

А вот и секретный ингредиент. Эту строку нужно разбирать по частям.

Первая часть: производная

nonlin(l1,True)

l1 представляет три этих точки, а код выдаёт наклон линий, показанных ниже. Заметьте, что при больших значениях вроде x=2.0 (зелёная точка) и очень малые, вроде x=-1.0 (фиолетовая) линии имеют небольшой уклон. Самый большой угол у точки х=0 (голубая). Это имеет большое значение. Также отметьте, что все производные лежат в пределах от 0 до 1.

Полное выражение: производная, взвешенная по ошибкам

l1_delta = l1_error * nonlin(l1,True)

Математически существуют более точные способы, но в нашем случае подходит и этот. l1_error – это матрица (4,1). nonlin(l1,True) возвращает матрицу (4,1). Здесь мы поэлементно их перемножаем, и на выходе тоже получаем матрицу (4,1), l1_delta.

Умножая производные на ошибки, мы уменьшаем ошибки предсказаний, сделанных с высокой уверенностью. Если наклон линии был небольшим, то в сети содержится либо очень большое, либо очень малое значение. Если догадка в сети близка к нулю (х=0, у=0,5), то она не особенно уверенная. Мы обновляем эти неуверенные предсказания и оставляем в покое предсказания с высокой уверенностью, умножая их на величины, близкие к нулю.

syn0 += np.dot(l0.T,l1_delta)

weight_update = input_value * l1_delta

Для крайнего левого веса это будет 1.0 * l1_delta. Предположительно, это лишь незначительно увеличит 9.5. Почему? Поскольку предсказание было уже достаточно уверенным, и предсказания были практически правильными. Небольшая ошибка и небольшой наклон линии означает очень небольшое обновление.

Но поскольку мы делаем групповую тренировку, указанный выше шаг мы повторяем для всех четырёх тренировочных примеров. Так что это выглядит очень похоже на изображение вверху. Так что же делает наша строчка? Она подсчитывает обновления весов для каждого веса, для каждого тренировочного примера, суммирует их и обновляет все веса – и всё одной строкой.

Понаблюдав за обновлением сети, вернёмся к нашим тренировочным данным. Когда и вход, и выход равны 1, мы увеличиваем вес между ними. Когда вход 1, а выход – 0, мы уменьшаем вес.

Вход Выход 0 0 1 0 1 1 1 1 1 0 1 1 0 1 1 0

Таким образом, в наших четырёх тренировочных примерах ниже, вес первого входа по отношению к выходу будет постоянно увеличиваться или оставаться постоянным, а два других веса будут увеличиваться и уменьшаться в зависимости от примеров. Этот эффект и способствует обучению сети на основе корреляций входных и выходных данных.

Часть 2: задачка посложнее

Вход Выход 0 0 1 0 0 1 1 1 1 0 1 1 1 1 1 0

Попробуем предсказать выходные данные на основе трёх входных столбцов данных. Ни один из входных столбцов не коррелирует на 100% с выходным. Третий столбец вообще ни с чем не связан, поскольку в нём всю дорогу содержатся единицы. Однако и тут можно увидеть схему – если в одном из двух первых столбцов (но не в обоих сразу) содержится 1, то результат также будет равен 1.

Это нелинейная схема, поскольку прямого соответствия столбцов один к одному не существует. Соответствие строится на комбинации входных данных, столбцов 1 и 2.

Интересно, что распознавание образов является очень похожей задачей. Если у вас есть 100 картинок одинакового размера, на которых изображены велосипеды и курительные трубки, присутствие на них определённых пикселей в определённых местах не коррелирует напрямую с наличием на изображении велосипеда или трубки. Статистически их цвет может казаться случайным. Но некоторые комбинации пикселей не случайны – те, что формируют изображение велосипеда (или трубки).

Стратегия

Чтобы скомбинировать пиксели в нечто, у чего может появиться однозначное соответствие с выходными данными, нужно добавить ещё один слой. Первый слой комбинирует вход, второй назначает соответствие выходу, используя в качестве входных данных выходные данные первого слоя. Обратите внимание на таблицу.

Вход (l0) Скрытые веса (l1) Выход (l2) 0 0 1 0.1 0.2 0.5 0.2 0 0 1 1 0.2 0.6 0.7 0.1 1 1 0 1 0.3 0.2 0.3 0.9 1 1 1 1 0.2 0.1 0.3 0.8 0

Случайным образом назначив веса, мы получим скрытые значения для слоя №1.

Интересно, что у второго столбца скрытых весов уже есть небольшая корреляция с выходом. Не идеальная, но есть. И это тоже является важной частью процесса тренировки сети. Тренировка будет только усиливать эту корреляцию.

Она будет обновлять syn1, чтобы назначить её соответствие выходным данным, и syn0, чтобы лучше получать данные со входа.

Нейросеть в три слоя

import numpy as np def nonlin(x,deriv=False): if(deriv==True): return x*(1-x) return 1/(1+np.exp(-x)) X = np.array([[0,0,1], [0,1,1], [1,0,1], [1,1,1]]) y = np.array([[0], [1], [1], [0]]) np.random.seed(1) syn0 = 2*np.random.random((3,4)) — 1 syn1 = 2*np.random.random((4,1)) — 1 for j in xrange(60000): l0 = X l1 = nonlin(np.dot(l0,syn0)) l2 = nonlin(np.

dot(l1,syn1)) l2_error = y — l2 if (j% 10000) == 0: print «Error:» + str(np.mean(np.abs(l2_error))) l2_delta = l2_error*nonlin(l2,deriv=True) l1_error = l2_delta.dot(syn1.T) l1_delta = l1_error * nonlin(l1,deriv=True) syn1 += l1.T.dot(l2_delta) syn0 += l0.T.dot(l1_delta) Error:0.496410031903 Error:0.00858452565325 Error:0.00578945986251 Error:0.00462917677677 Error:0.

00395876528027 Error:0.00351012256786

Переменные и их описания

X — матрица входного набор данных; строки – тренировочные примерыy – матрица выходного набора данных; строки – тренировочные примерыl0 – первый слой сети, определённый входными даннымиl1 – второй слой сети, или скрытый слойl2 – финальный слой, это наша гипотеза.

По мере тренировки должен приближаться к правильному ответуsyn0 – первый слой весов, Synapse 0, объединяет l0 с l1.syn1 – второй слой весов, Synapse 1, объединяет l1 с l2.l2_error – промах сети в количественном выраженииl2_delta – ошибка сети, в зависимости от уверенности предсказания.

Почти совпадает с ошибкой, за исключением уверенных предсказанийl1_error – взвешивая l2_delta весами из syn1, мы подсчитываем ошибку в среднем/скрытом слое

l1_delta – ошибки сети из l1, масштабируемые по увеернности предсказаний. Почти совпадает с l1_error, за исключением уверенных предсказаний

Код должен быть достаточно понятным – это просто предыдущая реализация сети, сложенная в два слоя один над другим. Выход первого слоя l1 – это вход второго слоя. Что-то новое есть лишь в следующей строке.

l1_error = l2_delta.dot(syn1.T)

Использует ошибки, взвешенные по уверенности предсказаний из l2, чтобы подсчитать ошибку для l1. Получаем, можно сказать, ошибку, взвешенную по вкладам – мы подсчитываем, какой вклад в ошибки в l2 вносят значения в узлах l1. Этот шаг и называется обратным распространением ошибок. Затем мы обновляем syn0, используя тот же алгоритм, что и в варианте с нейросетью из двух слоёв.

Источник: ХабраХабр

Нейросеть на Python, часть 1

Источник: http://max.horosh.ru/python-neural-network-1/

Нейронная сеть на Python с нуля своими руками | OTUS

Для начинающего Data Scientist-а очень важно понять внутреннюю структуру нейронной сети. Это руководство поможет вам создать собственную сеть с нуля, не используя для этого сложных учебных библиотек, к коим относится, например, TensorFlow. Материал написан на основании статьи американского учёного Джеймса Лоя (Технологический университет штата Джорджия).

Что такое нейронная сеть?

Очень часто в статьях по нейронным сетям авторы описывают их, проводя параллели с мозгом. Описать нейронную сеть можно и в качестве математической функции, отображающей заданный вход в желаемый результат.

Итак, нейронные сети включают в себя следующие компоненты:— х, входной слой;— ŷ, выходной слой;— набор весов и смещений между каждым слоем W и b;— произвольное количество скрытых слоев;— выбор функции активации для любого скрытого слоя σ (в данной статье будем использовать функцию активации Sigmoid).На диаграмме, представленной ниже, отображена архитектура 2-слойной нейронной сети (учтите, что входной уровень, как правило, исключается во время подсчёта числа слоев).

Идём дальше. Создание класса Neural Network на «Питоне» выглядит следующим образом:

class NeuralNetwork: def __init__(self, x, y): self.input = x self.weights1 = np.random.rand(self.input.shape[1],4) self.weights2 = np.random.rand(4,1) self.y = y self.output = np.zeros(y.shape)

Обучение нейронной сети

Выход ŷ простой 2-слойной нейронной сети: В уравнении, которое приведено выше, веса W и смещения b — единственные переменные, влияющие на выход ŷ. Разумеется, правильные значения для смещений и весов определяют точность предсказаний. А сам процесс тонкой настройки смещений и весов на основании входных данных называют обучением нейронной сети.

В обучающем процессе каждая итерация включает ряд шагов:1) вычисление прогнозируемого выхода ŷ (прямого распространения);2) обновление смещений и весов (обратное распространение).

Процесс обучения хорошо иллюстрирует последовательный график:

Прямое распространение

Как видно на графике, прямым распространением называют несложное вычисление, причём для базовой двухслойной нейронной сети вывод задаётся следующей формулой: Давайте теперь добавим в наш код функцию прямого распространения. Для простоты предполагается, что смещения равны нулю.

class NeuralNetwork: def __init__(self, x, y): self.input = x self.weights1 = np.random.rand(self.input.shape[1],4) self.weights2 = np.random.rand(4,1) self.y = y self.output = np.zeros(self.y.shape) def feedforward(self): self.layer1 = sigmoid(np.dot(self.input, self.weights1)) self.output = sigmoid(np.dot(self.layer1, self.weights2))

Чтобы оценить «добротность» наших прогнозов, воспользуемся функцией потери.

Функция потери

Вообще, существует много доступных функций потерь, и на выбор влияет характер нашей проблемы. Мы же будем применять в качестве функции потери сумму квадратов ошибок: Суммой квадратов ошибок называют среднее значение разницы между каждым фактическим и прогнозируемым значением. Что касается цели обучения, то она как раз в том и состоит, чтобы найти набор смещений и весов, который минимизирует вышеупомянутую функцию потери.

Обратное распространение

Когда ошибка нашего прогноза, то есть потери, измерены, необходимо отыскать способ обратного распространения ошибки, обновив смещения и веса. И чтобы узнать подходящую нам сумму, нужную для корректировки смещений и весов, требуется знать производную функцию потери по отношению к смещениям и весам.

Здесь давайте вспомним, что производной функции называют тангенс угла наклона функции. Раз есть производная, можно просто обновить смещения и веса, уменьшив либо увеличив их (смотрите диаграмму выше). Это называют градиентным спуском.

Однако мы не сможем непосредственно посчитать производную функции потерь по отношению к смещениям и весам, ведь уравнение функции потерь не включает в себя смещения и веса. На помощь приходит правило цепи: Да, это было громоздко, зато позволило нам получить то, что необходимо — производную функции потерь (наклон) по отношению к весам. А значит, можно регулировать веса.

Теперь добавим в наш код функцию обратного распространения (backpropagation):

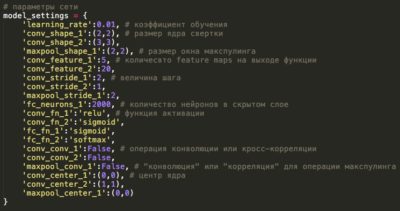
class NeuralNetwork: def __init__(self, x, y): self.input = x self.weights1 = np.random.rand(self.input.shape[1],4) self.weights2 = np.random.rand(4,1) self.y = y self.output = np.zeros(self.y.shape) def feedforward(self): self.layer1 = sigmoid(np.dot(self.input, self.weights1)) self.output = sigmoid(np.dot(self.layer1, self.weights2)) def backprop(self): # application of the chain rule to find derivative of the loss function with respect to weights2 and weights1 d_weights2 = np.dot(self.layer1.T, (2*(self.y — self.output) * sigmoid_derivative(self.output))) d_weights1 = np.dot(self.input.T, (np.dot(2*(self.y — self.output) * sigmoid_derivative(self.output), self.weights2.T) * sigmoid_derivative(self.layer1))) # update the weights with the derivative (slope) of the loss function self.weights1 += d_weights1 self.weights2 += d_weights2

Проверка работы нейронной сети

Когда полный код для выполнения обратного и прямого распространения есть, можно рассмотреть нейросеть на примере и посмотреть, как всё работает. На картинке вы видите идеальный набор весов. И наша нейронная сеть должна изучить его.

Давайте потренируем сеть на 1500 итераций. Рассматривая график потерь на итерациях, можно заметить, что потеря монотонно уменьшается до минимума. Всё это соответствует алгоритму спуска градиента, о котором уже упоминали.

Теперь посмотрим на вывод (окончательное предсказание) после 1500 итераций:

Итак, мы сделали это! Алгоритм обратного и прямого распространения показал успешную работу нейросети, а сами предсказания сходятся на истинных значениях. Но нужно добавить, что существует незначительная разница между фактическими значениями и предсказаниями. Это нормально и даже желательно, т. к. предотвращается переобучение, позволяя нейросети лучше обобщать невидимые данные.

Источник: https://otus.ru/nest/post/736/

Простая нейронная сеть в 9 строчек кода на Python

Из статьи вы узнаете, как написать свою простую нейросеть на python с нуля, не используя никаких библиотек для нейросетей. Если у вас еще нет своей нейронной сети, вот всего лишь 9 строчек кода:

Перед вами перевод поста How to build a simple neural network in 9 lines of Python code, автор — Мило Спенсер-Харпер. Ссылка на оригинал — в подвале статьи.

В статье мы разберем, как это получилось, и вы сможете создать свою собственную нейронную сеть на python. Также будут показаны более длинные и красивые версии кода.

Диаграмма 1

Но для начала, что же такое нейронная сеть? Человеческий мозг состоит из 100 миллиарда клеток, называемых нейронами, соединенных синапсами. Если достаточное количество синаптичеких входов возбуждены, то и нейрон тоже становится возбужденным. Этот процесс также называется “мышление”.

Мы можем смоделировать этот процесс, создав нейронную сеть на компьютере. Не обязательно моделировать всю сложную модель человеческого мозга на молекулярном уровне, достаточно только высших правил мышления. Мы используем математические техники называемые матрицами, то есть просто сетки с числами. Чтобы сделать все максимально просто, построим модель из трех входных сигналов и одного выходного.

Мы будем тренировать нейрон на решение задачи, представленной ниже.

Первые четыре примера назовем тренировочной выборкой. Вы сможете выделить закономерность? Что должно стоять на месте “?”

Диаграмма 2. Input — входный сигнал, Output — выходной сигнал.

Вероятно вы заметили, что выходной сигнал всегда равен самой левой входной колонке. Таким образом ответ будет 1.

Процесс обучения нейронной сети

Как же должно происходить обучение нашего нейрона, чтобы он смог ответить правильно? Мы добавим каждому входу вес, который может быть положительным или отрицательным числом. Вход с большим положительным или большим отрицательным весом сильно повлияет на выход нейрона. Прежде чем мы начнем, установим каждый вес случайным числом. Затем начнем обучение:

1. Берем входные данные из примера обучающего набора, корректируем их по весам и передаем по специальной формуле для расчета выхода нейрона.
2. Вычисляем ошибку, которая является разницей между выходом нейрона и желаемым выходом в примере обучающего набора.
3. В зависимости от направления  ошибки слегка отрегулируем вес.
4. Повторите этот процесс 10 000 раз.

Диаграмма 3

В конце концов вес нейрона достигнет оптимального значения для тренировочного набора. Если мы позволим нейрону «подумать» в новой ситуации, которая сходна с той, что была в обучении, он должен сделать хороший прогноз.

Формула для расчета выхода нейрона

Вам может быть интересно, какова специальная формула для расчета выхода нейрона? Сначала мы берем взвешенную сумму входов нейрона, которая:

Затем мы нормализуем это, поэтому результат будет между 0 и 1. Для этого мы используем математически удобную функцию, называемую функцией Sigmoid:

Если график нанесен на график, функция Sigmoid рисует S-образную кривую.

Подставляя первое уравнение во второе, получим окончательную формулу для выхода нейрона:

Возможно, вы заметили, что мы не используем пороговый потенциал для простоты.

Формула для корректировки веса

Во время тренировочного цикла (Диаграмма 3) мы корректируем веса. Но насколько мы корректируем вес? Мы можем использовать формулу «Взвешенная по ошибке» формула

Почему эта формула? Во-первых, мы хотим сделать корректировку пропорционально величине ошибки. Во-вторых, мы умножаем на входное значение, которое равно 0 или 1. Если входное значение равно 0, вес не корректируется. Наконец, мы умножаем на градиент сигмовидной кривой (диаграмма 4). Чтобы понять последнее, примите во внимание, что:

1. 1. Мы использовали сигмовидную кривую для расчета выхода нейрона.
   2. Если выходной сигнал представляет собой большое положительное или отрицательное число, это означает, что нейрон так или иначе был достаточно уверен.
   3. Из Диаграммы 4 мы можем видеть, что при больших числах кривая Сигмоида имеет небольшой градиент.

1. Если нейрон уверен, что существующий вес правильный, он не хочет сильно его корректировать. Умножение на градиент сигмовидной кривой делает именно это.

Градиент Сигмоды получается, если посчитать взятием производной:

Вычитая второе уравнение из первого получаем итоговую формулу:

Существуют также другие формулы, которые позволяют нейрону учиться быстрее, но приведенная имеет значительное преимущество: она простая.

Написание Python кода

Хоть мы и не будем использовать библиотеки с нейронными сетями, мы импортируем 4 метода из математической библиотеки numpy. А именно:

• exp — экспоненцирование
• array — создание матрицы
• dot — перемножения матриц
• random — генерация случайных чисел

Например, мы можем использовать array() для представления обучающего множества, показанного ранее.

“.T” — функция транспонирования матриц. Итак, теперь мы готовы для более красивой версии исходного кода. Заметьте, что на каждой итерации мы обрабатываем всю тренировочную выборку одновременно.

Код также доступен на гитхабе. Если вы используете Python3 нужно заменить xrange на range.

Заключительные мысли

Попробуйте запустить нейросеть, используя команду терминала:

python main.py

Итоговый должен быть похож на это:

У нас получилось! Мы написали простую нейронную сеть на Python!

Сначала нейронная сеть присваивала себе случайные веса, а затем обучалась с использованием тренировочного набора. Затем нейросеть рассмотрела новую ситуацию [1, 0, 0] и предсказала 0.99993704. Правильный ответ был 1. Так очень близко!

Традиционные компьютерные программы обычно не могут учиться. Что удивительного в нейронных сетях, так это то, что они могут учиться, адаптироваться и реагировать на новые ситуации. Так же, как человеческий разум.

Конечно, это был только 1 нейрон, выполняющий очень простую задачу. А если бы мы соединили миллионы этих нейронов вместе?

Источник: https://neurohive.io/ru/tutorial/prostaja-nejronnaja-set-python/

Собственная нейронная сеть. Просто как дважды два

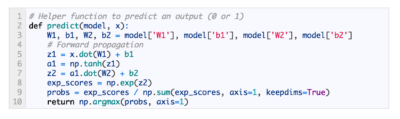
Многие хотят написать свою нейросеть, но теряются в тоннах книг по машинному обучению, и сложных математических формулах. Сегодня я покажу вам относительно простой пример нейросети на Python, который работает просто и понятно.

Есть множество разных видов нейросетей, и целей для которых они служат. В общем случае схема работы нейросети такова:

• Создают программу используя библиотеки для построения нейросетей
• Обучают программу на БОЛЬШОМ наборе данных, то есть дают ей набор данных, правильно размеченный человеком, чтобы нейросеть обучилась и начала работать на других похожих наборах данных
• Сохраняют и используют обученную нейросеть

Я в своем примере совместил обучение нейросети вместе с ее тестированием, поэтому при каждом запуске нейросеть сперва обучается(что занимает некоторое время, не думайте что программа зависла). Если вы захотите использовать данный пример в своих проектах то разделите скрипт на две части — первая будет обучать модель и сохранять её, а вторая работать на основе уже сохраненной модели. Подробнее о сохранении и загрузке моделей можно почитать тут.

К тому же в моем примере я буду использовать очень маленький набор данных, в реальных проектах набор данных должен быть минимум из нескольких тысяч строк.

Итак, мы создадим нейросеть которая пытается угадать какой тип контента нужно найти для пользователя, в ответ на его вопрос. Например, если пользователь спросит «Кто такой Виктор Цой», нейросеть должна ответить «Информация о личности». Она не будет отвечать на вопрос, просто классифицирует вопрос в определенную категорию. Обучающий набор данных очень маленький поэтому тестировать будем на более-менее похожих вопросах.

Сперва создадим набор данных для обучения. У меня это обычный текстовый файл в котором лежат строки, разделенные значком @. Назовите файл 1.txt и положите его рядом со скриптом нейросети. Используйте кодировку UTF-8.

Образец файла (отрывок)

Что такое патока @ Информация о предметеГде живут медведи @ МестоположениеКак зовут сына Трампа @ ИмяКак зовут Мадонну @ ИмяКак зовут Бьорк @ ИмяПочему небо голубое @ Информация о предметеКак сварить борщ @ ИнструкцияКак научиться летать @ ИнструкцияСколько звезд на небе @ КоличествоКто такая Мадонна @ Информация о личностиКакая высота у Эйфелевой башни @ КоличествоДата рождения Путина @ Дата рожденияКогда началась вторая Мировая война @ Дата событияКогда родился Майкл Джексон @ Дата рожденияПочему идет дождь @ Информация о предметеВ каких фильмах играл Ди Каприо @ Информация о предметеКогда родился Эйнштейн @ Дата рожденияКакой город начинает упоминаться с 1147 года @ ДатаЧто такое «дождь» @ Информация о предметеКто основал Санкт-Петербург @ ИмяКто такой Христофор Колумб @ Информация о личностиКак звали Колумба @ ИмяКакой страной управляет королева Елизавета II @ МестоположениеКакова средняя глубина Тихого океана @ КоличествоКакова высота Биг Бена @ КоличествоВ какой стране столицей является город Москва @ Местоположение

Полная версия файла для обучения нейросети

Установка модулей для Ubuntu

sudo apt install python3-pip

Скачиваем и распаковываем PyStemmer-1.3.0.tar.gz с сайта https://pypi.python.org/pypi/PyStemmer/1.3.0 в папку pystemmer.

cd pystemmer/sudo python3 setup.py installcd ..pip3 install numpypip3 install sklearnpip3 install scipy

Важно, запускается это чудо командой python3

Теперь покажу сам скрипт нейросети для классификации вопросов.

Код

Файл main.py — листинг кода

# -*- coding: utf-8 -*- import sysimport numpy as npimport pickleimport refrom Stemmer import Stemmerfrom sklearn.feature_extraction.text import TfidfVectorizerfrom sklearn.linear_model import SGDClassifierfrom sklearn.pipeline import Pipelinefrom sklearn.metrics import accuracy_score # — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — # очистка текста с помощью regexp приведение слов в инфинитив и нижний регистр, замена цифрdef text_cleaner(text): text = text.lower() # приведение в lowercase stemmer = Stemmer('russian') text = ' '.join( stemmer.stemWords( text.split() ) ) text = re.sub( r'\b\d+\b', ' digit ', text ) # замена цифр return text # — — — — — — — — — — — — — — — — — — — — — — — — -# загрузка данных из файла 1.txt# def load_data(): data = { 'text':[],'tag':[] } for line in open('1.txt'): if(not('#' in line)): row = line.split(«@») data['text'] += [row[0]] data['tag'] += [row[1]] return data # — — — — — — — — — — — — — — — — — — — — — — — — -# Обучение нейросети def train_test_split( data, validation_split = 0.1): sz = len(data['text']) indices = np.arange(sz) np.random.shuffle(indices) X = [ data['text'][i] for i in indices ] Y = [ data['tag'][i] for i in indices ] nb_validation_samples = int( validation_split * sz ) return { 'train': { 'x': X[:-nb_validation_samples], 'y': Y[:-nb_validation_samples] }, 'test': { 'x': X[-nb_validation_samples:], 'y': Y[-nb_validation_samples:] } } # — — — — — — — — — — — — — — — — — — — — def openai(): data = load_data() D = train_test_split( data ) text_clf = Pipeline([ ('tfidf', TfidfVectorizer()), ('clf', SGDClassifier(loss='hinge')), ]) text_clf.fit(D['train']['x'], D['train']['y']) predicted = text_clf.predict( D['train']['x'] ) # Начало тестирования программы z=input(«Введите вопрос без знака вопроса на конце: «) zz=[] zz.append(z) predicted = text_clf.predict( zz ) print(predicted[0]) # — — — — — — — — — — — — — — — — — — — — if __name__ == '__main__': sys.exit( openai() )

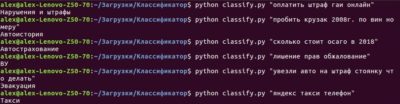
Давайте запустим нашу нейросеть, подождем пока она обучится и предложит нам ввести вопрос. Введем вопрос которого нет в обучающем файле — «Кто придумал ракету». Писать нужно без знака вопроса на конце. В ответ нейросеть выдаст «Имя», значит она определила что наш вопрос подразумевает ответ в котором должно быть чье-то имя. Заметьте, данного вопроса не было в файле 1.txt но нейросеть безошибочно определила что мы имеем ввиду, исходя из обучающей выборки.

Данный классификатор очень прост. Вы можете подать на вход в файл 1.txt абсолютно любые данные которые нужно классифицировать, это не обязательно должны быть вопросы и их категории как в моем примере.

Демонстрация работы скрипта

Материал об этой очень интересной разработке подготовил @pythono
Скрипт мною лично запущен и протестирован, что вы можете видеть на видео выше:)

Что с этим можно сделать

Источник: https://golos.io/vox-populi/@vp-webdev/sobstvennaya-neironnaya-set-prosto-kak-dvazhdy-dva

Основы Python

Нейросети создают и обучают в основном на языке Python. Поэтому очень важно иметь базовые представления о том, как писать на нем программы. В этой статье я кратко и понятно расскажу об основных понятиях этого языка: переменных, функциях, классах и модулях.

Материал рассчитан на людей, не знакомых с языками программирования.

Для начала Python надо установить. Затем нужно поставить удобную среду для написания программ на Python. Этим двум шагам посвящена отдельная статья на портале.

Если все установлено и настроено, можно начинать.

Поехали!

Переменные

Переменная — ключевое понятие в любом языке программирования (и не только в них). Проще всего представить переменную в виде коробки с ярлыком. В этой коробке хранится что-то (число, матрица, объект, …) представляющее для нас ценность.

Например, мы хотим создать переменную x, которая должна хранить значение 10. В Python код создания этой переменной будет выглядеть так:

x = 10

Слева мы объявляем переменную с именем x. Это равносильно тому, что мы приклеили на коробку именной ярлык. Далее идет знак равенства и число 10. Знак равенства здесь играет необычную роль. Он не означает, что «x равно 10». Равенство в данном случае кладет число 10 в коробку. Если говорить более корректно, то мы присваиваем переменной x число 10.

Теперь, в коде ниже мы можем обращаться к этой переменной, также выполнять с ней различные действия.

Можно просто вывести значение этой переменной на экран:

x=10 print(x)

С переменными, которые хранят числа, можно выполнять различные простейшие действия: складывать, вычитать, умножать, делить и возводить в степень.

x = 2 y = 3 # Сложение z = x + y print(z) # 5 # Разность z = x — y print(z) # -1 # Произведение z = x * y print(z) # 6 # Деление z = x / y print(z) # 0.66666… # Возведение в степень z = x ** y print(z) # 8

В коде выше мы вначале создаем две переменные, содержащие 2 и 3. Затем создаем переменную z, которая хранит результат операции с x и y и выводит результаты в консоль. На этом примере хорошо видно, что переменная может менять свое значение в ходе выполнения программы. Так, наша переменная z меняет свое значение аж 5 раз.

Функции

Иногда возникает необходимость много раз выполнять одни и те же действия. Например, в нашем проекте нужно часто выводить 5 строчек текста.

«Это очень важный текст!»«Этот текст нильзя ни прочитать»«Ошибка в верхней строчке допущена специально»«Привет и пока»

«Конец»

Наш код будет выглядеть так:

x = 10 y = x + 8 — 2 print(«Это очень важный текст!») print(«Этот текст нильзя не прочитать») print(«Ошибка в верхней строчке допущена специально») print(«Привет и пока») print(«Конец») z = x + y print(«Это очень важный текст!») print(«Этот текст нильзя не прочитать») print(«Ошибка в верхней строчке допущена специально») print(«Привет и пока») print(«Конец») test = z print(«Это очень важный текст!») print(«Этот текст нильзя не прочитать») print(«Ошибка в верхней строчке допущена специально») print(«Привет и пока») print(«Конец»)

Выглядит все это очень избыточно и неудобно. Кроме того, во второй строчке допущена ошибка. Ее можно исправить, но исправлять придется сразу в трех местах. А если у нас в проекте эти пять строчек вызываются 1000 раз? И все в разных местах и файлах?

Специально для случаев, когда необходимо часто выполнять одни и те же команды, в языках программирования можно создавать функции.

Задается функция с помощью ключевого слова def . Далее следует название функции, затем скобки и двоеточие. Дальше с отступом надо перечислить действия, которые будут выполнены при вызове функции.

def print_5_lines(): print(«Это очень важный текст!») print(«Этот текст нильзя не прочитать») print(«Ошибка в верхней строчке допущена специально») print(«Привет и пока») print(«Конец»)

Теперь мы определили функцию print_5_lines(). Теперь, если в нашем проекте нам в очередной раз надо вставить пять строчек, то мы просто вызываем нашу функцию. Она автоматически выполнит все действия.

# Определяем функцию def print_5_lines(): print(«Это очень важный текст!») print(«Этот текст нильзя не прочитать») print(«Ошибка в верхней строчке допущена специально») print(«Привет и пока») print(«Конец») # Код нашего проекта x = 10 y = x + 8 — 2 print_5_lines() z = x + y print_5_lines() test = z print_5_lines()

Удобно, не правда ли? Мы серьезно повысили читаемость кода. Кроме того, функции хороши еще и тем, что если вы хотите изменить какое-то из действий, то достаточно подправить саму функцию. Это изменение будет работать во всех местах, где вызывается ваша функция. То есть мы можем исправить ошибку во второй строчке выводимого текста («нильзя» > «нельзя») в теле функции. Правильный вариант автоматически будет вызываться во всех местах нашего проекта.

Функции с параметрами

Просто повторять несколько действий конечно удобно. Но это еще не все. Иногда мы хотим передать какую-ту переменную в нашу функцию. Таким образом, функция может принимать данные и использовать их в процессе выполнения команд.

Переменные, которые мы передаем в функцию, называются аргументами.

Напишем простую функцию, которая складывает два данных ей числа и возвращает результат.

def sum(a, b): result = a + b return result

Первая строчка выглядит почти так же, как и обычные функции. Но между скобок теперь находятся две переменные. Это параметры функции. Наша функция имеет два параметра (то есть принимает две переменные).

Параметры можно использовать внутри функции как обычные переменные. На второй строчке мы создаем переменную result, которая равна сумме параметров a и b. На третьей строчке мы возвращаем значение переменной  result.

Теперь, в дальнейшем коде мы можем писать что-то вроде:

new = sum(2, 3) print(new)

Мы вызываем функцию sum и по очереди передаем ей два аргумента: 2 и 3. 2 становится значением переменной a, а 3 становится значением переменной b. Наша функция возвращает значение (сумму 2 и 3), и мы используем его для создания новой переменной new.

Запомните. В коде выше числа 2 и 3 — аргументы функции sum. А в самой функции  sum переменные a и b — параметры. Другими словами, переменные, которые мы передаем функции при ее вызове называются аргументами. А вот внутри функции эти переданные переменные называются параметрами. По сути, это два названия одного и того же, но путать их не стоит.

def square(a): return a * a

Наша функция состоит всего из одной строчки. Она сразу возвращает результат умножения параметра a на a.

Я думаю вы уже догадались, что вывод данных в консоль мы тоже производим с помощью функции. Эта функция называется print() и она выводит в консоль переданный ей аргумент: число, строку, переменную.

Массивы

Если переменную можно представлять как коробку, которая что-то хранит (не обязательно число), то массивы можно представить в виде книжных полок. Они содержат сразу несколько переменных. Вот пример массива из трех чисел и одной строки:

array = [1, 89, 3, «строка»]

Вот и пример, когда переменная содержит не число, на какой-то другой объект. В данном случае, наша переменная содержит массив. Каждый элемент массива пронумерован. Попробуем вывести какой-нибудь элемент массива:

array = [1, 89, 3, «строка»] print( array[1] )

В консоли вы увидите число 89. Но почему 89, а не 1? Все дело в том, что в Python, как и во многих других языках программирования, нумерация массивов начинается с 0. Поэтому array[1] дает нам второй элемент массива, а не первый. Для вызова первого надо было написать array[0].

Размер массива

Иногда бывает очень полезно получить количество элементов в массиве. Для этого можно использовать функцию len(). Она сама подсчитает количество элементов и вернет их число.

array = [1, 89, 3, «строка»] print( len(array) )

В консоли выведется число 4.

Условия и циклы

По умолчанию любые программы просто подряд выполняют все команды сверху вниз. Но есть ситуации, когда нам необходимо проверить какое-то условие, и в зависимости от того, правдиво оно или нет, выполнить разные действия.

Кроме того, часто возникает необходимость много раз повторить практически одинаковую последовательность команд.

В первой ситуации помогают условия, а во второй — циклы.

Условия

Условия нужны для того, чтобы выполнить два разных набора действий в зависимости от того, истинно или ложно проверяемое утверждение.

В Python условия можно записывать с помощью конструкции if: … else: …. Пусть у нас есть некоторая переменная x = 10. Если x меньше 10, то мы хотим разделить x на 2. Если же x больше или равно 10, то мы хотим создать другую переменную new, которая равна сумме x и числа 100. Вот так будет выглядеть код:

x = 10 if(x < 10): x = x / 2 print(x) else: new = x + 100 print(new)

После создания переменной x мы начинаем записывать наше условие.

Начинается все с ключевого слова if (в переводе с английского «если»). В скобках мы указываем проверяемое выражение. В данном случае мы проверяем, действительно ли наша переменная x меньше 10. Если она действительно меньше 10, то мы делим ее на 2 и выводит результат в консоль.

Затем идет ключевое слово else, после которого начинается блок действий, которые будут выполнены, если выражение в скобках после if ложное.

Если она больше или равна 10, то мы создаем новую переменную new, которая равна x + 100 и тоже выводим ее в консоль.

Циклы

Циклы нужны для многократного повторения действий. Предположим, мы хотим вывести таблицу квадратов первых 10 натуральных чисел. Это можно сделать так.

print(«Квадрат 1 равен » + str(1**2)) print(«Квадрат 2 равен » + str(2**2)) print(«Квадрат 3 равен » + str(3**2)) print(«Квадрат 4 равен » + str(4**2)) print(«Квадрат 5 равен » + str(5**2)) print(«Квадрат 6 равен » + str(6**2)) print(«Квадрат 7 равен » + str(7**2)) print(«Квадрат 8 равен » + str(8**2)) print(«Квадрат 9 равен » + str(9**2)) print(«Квадрат 10 равен » + str(10**2))

Пусть вас не удивляет тот факт, что мы складываем строки. «начало строки» + «конец» в Python означает просто соединение строк: «начало строкиконец». Так же и выше мы складываем строку «Квадрат x равен » и преобразованный с помощью функции str(x**2) результат возведения числа во 2 степень.

Выглядит код выше очень избыточно. А что, если нам надо вывести квадраты первых 100 чисел? Замучаемся выводить…

Цикл while повторяет необходимые команды до тех пор, пока остается истинным условие.

x = 1 while x

Источник: https://neuralnet.info/article/%D0%BE%D1%81%D0%BD%D0%BE%D0%B2%D1%8B-%D1%8F%D0%B7%D1%8B%D0%BA%D0%B0-python/